Play Like an Idiot

McCulloch-Pitts: “Purposive behavior depends upon how output affects input which, in turn, depends upon a nervous system whose organization can be treated statistically.”

SEER – McCULLOCH – LACAN

David Hagelbarger & Claude Shannon’s SEER (SEquence Extrapolating Robot)

The SEER (SEquence Extrapolating Robot) was developed by Claude Shannon & David Hagelbarger at the Bell Labs in the early 1950s. Its aim was to outplay a human in the game of odd or even (aka matching pennies or ones and twos), In the game the player has to guess if their opponent is holding one or two pennies (or marbles) in their hand. To personalize the playing experience the machine was made to resembled a human face with two lights for eyes, a button for the nose and a red toggle switch forming a tongue sticking out. This is in keeping with the playfulness of Shannon’s other machines, particularly the “ultimate machine” (1952), the only purpose of which was to switch itself off.

Over the years both Claude Shannon and David Hagelbarger worked on a variety of second guessing machines with various names, including the "Mind-Reading (?) Machine" and the "Outguessing Machine". SEER (SEquence Extrapolating Robot) was the title considered most scientifically respectable.

Operating diagram of Claude Shannon's Mind Reading Machine

David Hagelbarger (who built the first outguessing machine), with his device.

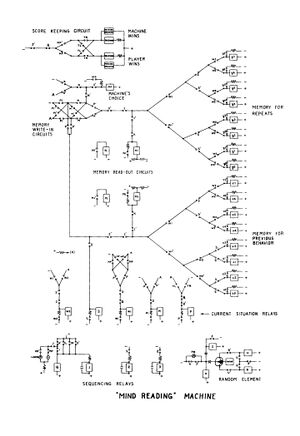
Underlining the machine's playful appearance and function were serious reasons to develop predictive machines: “We hope,” wrote Shannon, “that research in the design of game-playing machines will lead to insights in the manner of operation of the human brain”. Shannon noted at the time, as did Lacan and Guilbaud, that the game of matching pennies had already been used to model human predictive behavior in Von Neumann and Morgenstern’s Theory of Games and Economic Behavior and that the game had been a key figure in Edger Allen Poe’s Purloined Letter. Shannon & Hagelbarger also wanted to develop a machine that could readjust itself and adapt: “Perhaps in an extremely complicated situation it might be easier to design a machine which learns to be efficient than to design an efficient machine as such.”1 It was also useful, within the communications industry, to have machines that could execute complex actions with humans and other machines whilst using minimum processing power. In the case of SEER the processing power was minimal and yet it was able to produce complex behaviour in both human and machine, and furthermore, the complexity produced when the intersubjective space between human and machine. The machine had only 16 bits of storage (2 bytes) but was nevertheless able, in a game of long duration, to outguess its human opponent 65%-75% of the time. SEER gave a binary choice between “left” or “right”. In the first move the machine guessed randomly, after which it “learned” from the patterns produced by its opponent. Its choice of left or right would be dependent on the human opponent’s previous choice (its dossier of choices) and on a random choice.

The machine broke the penny-matching model down into eight scenarios, each with a particular probable outcome. For example: if the human player wins twice in a row with the same choice –let’s say “right”–, the human tendency would be to switch on the third move – to “left”–, because to stick with “right” would not be random. Such decisions were recorded as a “1” or “0” in SEER’s 16-bit memory. For each of the eight scenarios the machine recorded the last two only – filling the 16-bit memory. To predict its opponent’s move the machine would check the last two moves taken when the particular scenario in question occurred and choose the same. If the human opponent chose differently it would use a spinning commutator, which gave a random result.2

The human was likely to lose against SEER in the majority of cases because it was close to impossible for humans to counterfeit random choice. Shannon, however, notes that he was able to outguess SEER by getting into the “mind” of the machine, mentally emulating the machine’s operation and then doing the opposite. However, because the machine plays randomly, even a perfect human emulator could only ever win 75 % of the time.

In the later stages of the experiment the human factor was eliminated altogether, as Shannon & Hagelbarger had two outguessing machines play each other, with play invigilated by an “umpire” machine.

In March 1953 Claude Shannon wrote a Bell Laboratories memorandum entitled “A Mind-Reading (?) Machine” in which he noted that “[The game of matching pennies/ones and twos had been] discussed from the game theoretical point of view by von Neumann & Morgenstern and from a psychological point of view by Edger Allan Poe in his story The Purloined Letter. Oddly enough, the machine is aimed at Poe’s method rather than von Neumann’s.” In Poe’s story, the detective, Dupin, discusses the game of odd and even on the basis that people can be predicted even when they try not to be. Von Neumann & Morgenstern’s emphasis was on the role of random choice had on the player of the two-person sum-zero game. Lacan’s seminar and lecture addressed the complexity of both these positions. In Theory of Games and Economic Behavior (1944) Von Neumann & Morgenstern had proved mathematically that random choice becomes a defensive position if the two protagonists are evenly matched. If they are evenly matched the introduction of randomness will give the player acting randomly advantage. The machine (SEER) can, however, produce a true random result, which a human opponent to the machine can less readily do.

A source of amusement at the Bell Labs for Shannon & Hagelbarger was that the elite scientists who played with SEER understood it as a test of intelligence. It is the unconscious (non-conscious) structure of such a machine that renders it unbeatable. It was Lacan’s task to stress the importance of this to the participants in his second seminar.

We will see shortly that Lacan’s discourse on cybernetics continues with consideration of Von Neuman & Morgenstern’s s game theory and that the series of +s , –s , 0s and 1s were, for Lacan, units of probability which establish the syntax within a symbolic system.

From the early 1940s John Von Neuman had been keen to establish a relationship between the way a computer operates and the way the organic neural system operates. Von Neuman posited that a form of machine intelligence could be achieved if the machine was built on the principles of McCulloch-Pitts model of neuron activity. McCulloch-Pitts became the bridge between a cybernetic approach (which recognised a relation between the operations of servomechanisms and biological systems) and information theory, (which concentrated on the effectiveness of the message and the operations of “thinking machines”).

McCULLOCH – SEER– GOVERNOR–BRAIN

Cybernetician Warren McCulloch

For some years, Warren McCulloch had been arguing that the neurotic activity of the human brain could be reproduced in a machine. With John Von Neumann, McCulloch supported the idea that a "logic machine" could be build which exhibited the cognitive abilities of "perception, thought, memory, concept formation, knowledge of universals and their recognition, will, and even consciousness". and that the model for such a machine would be Allen Turing's theoretical Universal Turing Machine (1936). McCulloch put forward the notion that neural activity (thinking) was produced within a the network of circuits, cycles and loops. In 1930 Lawrence Kubie – then a neurophysiologist, before entering a career as a psychoanalyst – had proposed that neutrons behave in such a fashion; in 1938 Lorente de No demonstrated experimentally the existence of such cycles in the nervous system. McCulloch and Pitts paper, Ideas Immanent in Nervous Activity, mapped out this cycling activity in mathematical, probabilistic terms. In 1941 Kubie, now a psychoanalyst, posited that this cycling activity could be the basis for neurosis. This is made possible because as the these "reverberating circuits" allow the sequences of events that reach the nervous system, to be "captured and placed beyond the reach of time" , to be preserved in memory. Neurosis would be the cycling of such memories. This cybernetic reading of the compulsion (or automatism) was well known to Lacan, as we will discuss soon.

At the beginning of the 1950s, we were still some distance from a "thinking machine", the technical standard of the day was set by machines like SEER. In Warren S. McCulloch’s Machines That Think and Want (1950), McCulloch outlines the precise relation between a rudimentary 16-bit computer (such as SEER) and the human neural system. McCulloch proposes that we think of a neuron as “a telegraphic relay system which, tripped by a signal, emits another signal” this takes a millisecond, and again in line with a single state computer, “its signal is a briefer electrical impulse whose effect depends only on conditions where it ends, not where it begins. One signal or several may trip a relay, and one may prevent another from so doing.” McCulloch invites us to understand such signals as the atoms of a molecular event. “Each goes or does not go” (an all-or-none impulse). It can only signal that it was tripped, and its signal implies that it was tripped. “The signal received is an atomic proposition. It is the least event that can be true or false.” McCulloch next introduces a simple symbolic system to map these “atomic units”. The system is comprised of a series of Xs denoting a specific operation.

.X = A happens (a single neuron has been tripped)
X. = B happens
‘X = both happen
X, = neither happen
X = The signal of a neuron never tripped (contradiction).

The system describes several things.

1. the operations of a 16-bit computer (such as SEER)
2. the activities of neurons as units of probability
3. revealing 1. and 2. as essentially negentropic.

“Every next atomic event, depending on two present atomic events, is shown as a dotted X of which there are 16.” The calculus of propositions in such a scheme is 16. This is essentially the structure of SEER. The operation of each atomic event is linked to probability. If in a particular millisecond we are given ‘X , since its probability is ¼ its amount is 2 units [of information]” Any machine yet built cannot match the number of operations undertaken by the human brain. The Human brain is showered with a superabundance of stimuli which mostly fail to coincide. “Information measures the order of the ensemble in the same sense that entropy measures its chaos. In Wiener’s phrase, information is negative entropy; and our X’s the more the dots the greater the entropy.”

An elaboration of the scheme makes this clearer

"We reject a great deal more information than we receive; we see an agreement occurs in those instances where dots are absent” In this way information is adjustive and produces a filter with consolidates particular atomic events (‘x or x’ &c) “Circuits with negative feedback return a system toward an established state which is the end of the operation – its goal. Reflexes left to their own devices are thus homeostatic.”

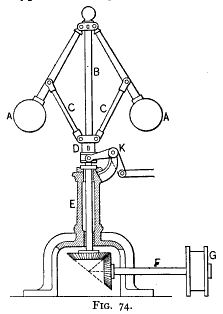
McCulloch next moves to establish a relation between homeostasis within the body and brain and the governor of the Steam Engine. Just as each receptor within the body serves to return a given perimeter to its established value, so within the brain the impulses through the thalamus to the cortex are inhibited through limits established by negative feedback. The response of the circuits passing through this system “depends on the time the returning meet the incoming signals”.

Some cycles resonate and oscillate, which may tend toward excitability and instability (positive feedback). Others regulate any such excitation, which results in homeostasis (negative feedback). The servomechanism most importantly operates on the information passing through the system regulated by negentropy, which guards against overrun or positive feedback. The starting point of which has been a series of Xs

The key point here, particularly as we go on to discuss Lacan’s Seminar II in greater detail, is that McCulloch has established an equivalence between the operations of a finite state computer, the operations of a servo mechanism and the operations of the human neural system. Lacan’s seminar was open to discussing the implications of this equivalence, incorporating Von Neumann & Morgenstern's Game Theory and Shannon's Information Theory to bind these connections.

As was discussed in a previous chapter, McCulloch had very little time for the discipline of psychoanalysis, and after establishing how neural activity (be it man-made or begotten) is organised, next makes a link to purpose.

McCulloch charts how the cycles which produce homeostasis in an organism also produce what we recognise as psychic activity.

“[P]urposive acts cease when they reach their ends. Only negative feedback so behaves and only it can set the link of the governor to any purpose. By it we enjoy appetites which, like records that extend memories, pass out of the body through the world and returning stop the initial eddies that sent them forth.” This process of what McCulloch terms “apititation” is manifold and may, like the involuntary actions of swallowing and breathing, be contradictory or “incommensurate”. The outcome of such conflict can be described as choice. ( In this way McCulloch links the operations of the governor to the operations of the psyche, suggesting an alternative to Freudian psychoanalysis (in which motivation is regulated by psychic energy). In McCulloch the circuit of “apititation” (desire?) is that of information; which links involuntary actions, such as breathing and swallowing, which are regulated by the same homeostatic circuits.

ODD OR EVEN? – LACAN

In a previous chapter we have discussed the implications of the cybernetic discourse for Lacan, particularly in relation Freud’s notion of dynamic psychology. We have also established how Lacan considered cybernetics to have had a substantial impact on discourse itself as we move from the discourse on knowledge to the discourse of the machine.

Indeed, the cybernetic discourse of homeostasis, circuitry and regulative feedback would continue be central to Lacan’s Seminar II as it progressed, as would the particular elements discussed in this and the previous chapters. In his analysis of Edger Allen Poe’s The Tale of the Purloined Letter, and in his lecture on Cybernetics and the Unconscious, Lacan would discuss Von Neumann & Morgenstern's Game Theory and Economic Behaviour; the game of odds & evens (which is discussed in both Poe’s story and in Von Neumann & Morgenstern's book). Lacan would also describe a “second guessing” finite state automata (similar to Shannon & Hagelbarger’s SEER) in order to outline the tendency of symbolic apparatus (be they begotten or man-made) to produce patterns which enter the circuitry of signification.

Lacan’s seminar on the Purloined letter, which takes up part of Seminar II, was a public manifestation of a dialogue that had been going on for some time, principally with the Author of What is Cybernetics? (1954) – who was also the co-organiser of the Paris congresses on cybernetics (1950-1951) – Georges Theodule Guilbaud.

Guilbaud’s “Lectures on the Principal Elements in the Mathematical Theory of Games” had earlier made explicit reference to Edger Allan Poe’s Purloined Letter. In various other texts Guilbaud notes the game of odd & even (ones & twos), mentioned in Poe’s tale as equivalent to Matching Pennies, the game cited for similar analysis by Neumann and Morgenstern in Theory of Games and Economic Behavior (1944). In Guilbaud’s lecture “Pilots, Planners, and Gamblers: Toward a Theory of Human Control”, Guilbard posits the idea that the game of Odds & Evens presents the possibility of the mathematicians’ dream – the pure game (jeu pur). In this lecture Guilbaud also cites an earlier work by Jacques Lacan, Logical Time and the Assertion of Anticipated Certainty, (1945) which discusses Neumann and Morgenstern’s Theory of Games and Economic Behavior no more than a year after its publication.
r For Lacan the game theory of Neumann and Morgenstern, the communications theory of Shannon and the notion of the (theoretical) universal machine conceived by Turing allowed for a wholly up-to-date conception of the unconscious By 1954, as Lacan opened his seminar, a particular kind of machine had emerged that both illustrated and performed the formation of the subject in exterior relation to the machinery of the game. It was specifically finite state automata such as the SEquence Extrapolating Robot (SEER) that allowed Lacan to claim that “the symbolic world is the world of the machine.” In the case of the tortoise and in the finite state automata, the same relation is established. Both machines – in their encoding and in their production of symbolic material (be they conscious or not) – demand an encounter with an other.

“...when one illustrates the phenomenon of language with something as formally purified as mathematical symbols - and that is one of the reasons for putting cybernetics on the agenda - when one gives a mathematical notation of the verbum, one demonstrates in the simplest possible way that language exists completely independently of us.”

Jacques Lacan’s Seminar II comes half a decade after French elite intellectuals were introduced to game theory, cybernetics and communication theory.

In Odd or even? Beyond Intersubjectivity, Lacan explains the function of a machine very similar to SEER, Lacan got participants to play odd or even (matching pennies) and to record the results (win or lose) as + or – symbols. The events follow a similar narrative to the one described by playing Shannon & Hagelbarger’s SEER.

Lacan unpacks his argument carefully and is, perhaps uncharacteristically, systematic in developing his argument. Lacan first introduces the game of odd and even as played in Poe’s story; he then outlines how people routinely play the game, “second-guessing” their opponent; he then outlines how a machine, lacking the capacity to “second guess”, might play the game differently. Lacan introduces the notion of randomness and the extreme difficulty the human subject has actually being random – in contrast to the unconscious machine. Lacan also introduces the idea of recording the results as + and – in the following configurations:

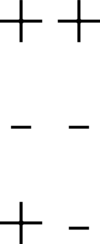
I reproduce this sequence here because it is important to illustrate that the minute you start to record the +s and –s in sequence, a pattern is established. This is a memory exterior to the subject. Lacan outlines how the game is played between two people and compares it to how a human plays against a “thinking machine”. In a human to human game a single play has no meaning (it makes no difference). There is no surprise if you hold the same (odd or even) as your opponent. In the first play you have a 50% chance of winning, on the second play a 25% by the third play you have a 12.5% of winning. You are soon caught in a play of difference where the odds decrease and the stakes rise with each play. The odds are produced by knowledge of the previous play, by knowing that the opponent knows you are caught in the chain of signification. The play produces a pattern of choices which amounts to a trail of probability, a record or memory of the game (which is why it was important for Lacan that a record of the + and – be kept when participents to the seminar played the game). Lacan points out that even at this early stage we have “left the domain of the real and entered realm of symbolic signification”. This is defined by the + &– and – &+ which record each move. The fact that the + & – is written brings the player into the realm of probability. For Lacan “the very notion of probability presupposes the introduction of the symbol into the real.” 10 The order of wins and losses only makes sense when they are written down in a sequence, if it is not written down, there is nothing to win; “the pact of the game is essential to the reality of the experience sought after.”

In the first few moves of odd and even, Lacan has raised three issues that will become central to our examination of his cybernetic discourse. The first is that the introduction of the symbolic into the domain of the real produces a circuit between signs, things and subjects. Secondly, Lacan stresses the centrality of probability; as the seminar progresses, the “conjectural science” of the 1600s become central to Lacan’s discourse of cybernetics – the period of conjectural science is when probability, which studied ratios of difference, emerged as a discipline. (see chapter eleven). The third issue is that the simple choice establishes a difference which establishes and consolidates order (the negentropic function of making a choice).

Lacan next considers what happens when a human plays the machine. Again the player must make a simple choice (a difference that makes a difference). The player must then inform the machine that they won or lost. Lacan then surmises the interior workings of the machine (sketching a mechanism very similar to SEER) which

a) records the results,
b) reacts to its opponent and
c) periodically randomises its response.

The player does not know the extent of the record kept by the machine or its ability to recall that information. Lacan notes that the machine will win by virtue of the human players exhaustion, as play progresses the human would not be able to calculate the machine’s next move without recourse to (ironically) an adding machine. This summation is similar to the accounts of the operations of SEER.

Lacan next hypothesises that a player might surmise that the machine is an equal match, that the machine is identical to the player. If this were the case the player would be the other to the machine. The machine would contain a “psychological profile” of its human opponent and would be capable of second guessing the human player. In such a case “a simple oscillation comes back” ordering the relation between machine and human, and the human player will resort to random choice – in this case the “psychological profile is completely eliminated”. Whether the machine plays like an idiot or an intelligent human, the human will make the same play. Here Lacan articulates a central premise of von Neumann & Morganstern’s sum-zero two-player game and the mischievous psychology wired into the circuitry of Shannon & Hagelbarger’s SEER.

So, irrespective of whether your opponent is an idiot or a genius, the next stage is to play at random. Lacan recalls a random action reported to Freud, which becomes the point of fixation. A number pulled out of a hat will quickly lead the subject “to that moment when he slept with his little sister, even to the extent that he failed his baccalaureate because that morning he had masturbated”Such a realisation will force the subject to understand that there actually is no such thing as chance. Without the subject being conscious of it “the symbols continue to mount one another, to copulate, to proliferate, to fertilise each other, to jump on each other, to tear each other apart”.

Extract a single particle, like a number from a hat, a “chance” particle which makes a screen on which to order memory. Here lies the difference between remembering (a definable property of living substance) and memory (the grouping and succession of symbolically defined events). Memory involves integrations – by which something new in the string of symbols will effect what went before. There is a retroactive effect which is “specific to the structure of symbolic memory, in other words to the function of remembering.”

Lacan comes back to the issue that, be it a machine or an idiot or an intelligent opponent, all that is needed for there to be a subject who asks a question is the quod: the demonstration of proof; the signal that the proof has been demonstrated (the + &–). It is on this quod that the interrogation bears.

Lacan prepares his class for the next session (The Purloined Letter), pointing out that, irrespective of the player’s intellectual acumen, after three goes it is best to play like an idiot – because after the third play: “everything loses its signification”.